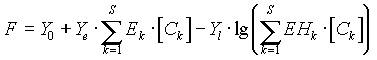
SIRKO is a general program for calculations associated with the study of chemical equilibria.The objective in using a program such as SIRKO is to obtain the equilibrium constants and quantities derived from them such a species concentrations under chosen conditions. A distinctive feature of our approach is the use of the universal response function applicable to very many different experimental technique. This allows analytical calculation of all necessary derivatives and weighting factors which increase the speed of our programm. This also allows the inclusion of any independent variable into the set of refinable parameters, which eliminates systematic errors.
Calculation of equilibrium constants can be performed with
various kinds of data. Often, a set of reagents is titrated and a
property of the mixtures is measured at each titration point. The
data obtained in this way is termed a titration curve. Or, the
measurements may be made on a series of individual solutions, in
which case the data are termed measurements. Both methods may be
used in this program.
It may be that this raw data is produced on a
microprocessor-controlled instrument so that it can be stored in
a data file. For certain makes of instrument, the file can be
directly imported into SIRKO:
For other instruments, an interface would need to be written, or
the experimental data entered by hand.
Any experimentally measured property may be used, if it can be
described by the general response function:
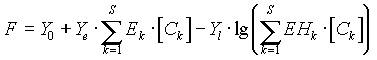
where F is the measured value,
S - number of components in solution
[Ck] - equilibrium concentration of the k-th component
Y0 - a constant value for a given method, often reflecting the
solvent properties
Yl - scaling factor for potentiometric methods
Ye - scaling factor for additive methods
Ek - physico-chemical parameter of the k-th component for
additive methods
EHk- parameter of the k-th component for potentiometric methods.
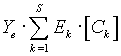 is the part which
describes additive methods- spectrophotometry, calorimetry, etc.
is the part which
describes additive methods- spectrophotometry, calorimetry, etc.
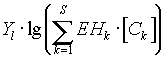 is the part
which describes potentiometric methods
is the part
which describes potentiometric methods
So, the response function used in our program describes well
practically any type of experiment for measuring stability
constants.
Thus, for spectrophotometry, having proposed Yl=0 and all EHi=0,
F will represent the optical density of the solution, Ei will
reflect the molar indices of absorption, Ye the thickness of the
cells, and Y0 the optical density of the solvent.
In calorimetric experiments, F is the quantity of heat released
or absorbed during the reaction, Ye the volume, and Ei the molar
enthalpy of the complex formation.
For potentiometric experiments, having defined Ye=0 and Ei=0, and
EHi=i ( where i is the activity coefficient of the ion for which
there is a reversible selective electrode) we obtain the ordinary
Nernst equation :![]()
Here F may represent either the potential in millivolts, in
which case Yl=S and Y0 is the zero potential, or in PCi=-lg[Ci]
for which Yl= and Y0=0, where characterises the deviation of the
electrode function from the theoretical Nernst equation. It is,
thus, possible to take into account the effect of an interfering
cation j, if EHj is the selectivity coefficient.
In addition, this function may describe the behaviour of the
electrode for pH measurement where it is often necessary to take
into account liquid potentials:
![]()
In this case, F should be considered as the measured values of
pH, Y0=pH0, where EH0 only for the proton for which EH= and E0
for proton (E=A) and hydroxyl (E=B).
Thus the chosen response function is universal and may be used
for any type of experiment. It is convenient when the
simultaneous processing of data from different experiments is
carried out.
Any experiment ("block") may be independant from the
athers and the equilibrium situation is altered for each block,
necessitating the calculation of equilibrium concentrations for
each block.
Alternatively the blocks may be dependant (for example
spectrophotometric measurements is a series of blocks and every
block represents a different wavelength). In this case, the
equilibrium concentrations are calculated only once and are
common between blocks.
The significant characteristic of our approach is that the
variables involved in the general response function (such as
Y0,Yl, Ek, EHk) may act both as model parameters and independent
variables. This is defined by the user. For example, when we are
calibrating an electrode for which we do not know the liquid
potential, then EHi and Ei should be considered as parameters and
refined. In any subsequent work with this electrode, they may
already be considered as independent variables. Similarly for
spectrophotometry, if from a single experiment one can determine
the molar absorption of a ligand, then Ei for the ligand can be
defined as a parameter while in other experiments this value
would be used as an independent variable.
It is rather simple for the user to change a variable between a
parameter and an independent variable. Each parameter is defined
with the key IP (index of refinement) which can adopt the values
0,1,2. If IP=0, then the corresponding value will not be refined,
and thus it acts as an independent variable, its dispersion
contributing to the weight factor according to the formula (32).
If IP=1 or 2 then the corresponding value is defined to be a
parameter and will be refined. Moreover, if IP=1, it is refined
only in one block. If IP=2, then this parameter is common for
some blocks. Thus, if we determine the electrode parameters from
a series of titration curves, and in some series the alkali
concentration is not known, then both alkali concentration and
electrode characteristics are model parameters. However, the
electrode parameters will be common for the series of titration
curves, while the alkali concentration will be common only for
the corresponding titration curve.
The refinement of additional parameters helps to eliminate
systematic errors, but here, they should be treated with caution,
because this often make the differences in models insignificant,
and so the refined parameters should be carefully scrutinised. In
any case, if some additional parameters correlate strongly with
other ones, then its value should be refined experimentally and
subsequently used as an independent variable.
The mathematical model of the equilibrium chemical system is
defined by the number of reagents, the reagent definitions and
the number of mass-balance equations (chemical reactions /
equilibria). Here, it is convenient to use a
formal-stoechiometric approach and to represent the reaction
mixture as a stoechiometric matrix. Element of which represent
stoechiometric coefficients of the reagent in the reaction. So,
for example, a model for system consists ligand, proton and
complexing cation may be defined by three equilibrium reactions :
L + H = LH K1=[LH]/[L]/[H]
L + M = LM K2=[LM]/[L]/[M]
L + H + M = LHM K3=[LHM]/[L]/[H]/[M]
Coresponding matrix:
1 1 0
1 0 1
1 1 1
The equilibrium constants calculated are the overall stability
constants (in log unit) The stepwise formation constant can be
obtained from the overall ones.
The determination of the model is best performed by comparing the
calculated errors for different models (see Section 3.7). It is,
therefore, important to try optimisation of constants for a
variety of model systems and to compare the results and errors.
For determination of equilibrium constant and additional
parameters (electrode parameters, initial analytic concentration,
e.t.c) we have used the least-squares method for which the best
parameters are those which minimise the weighted summation of the
squared deviation of the calculated values of the dependent
variable from the measured ones:
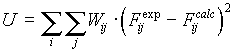
To minimise the function, singular Jacobian decomposition is
applied. This allows the analysis of the Jacobian matrix (Jw) for
conditionality. If matrix Jw is poorly conditioned, then at least
one of the singular numbers i will be considerably smaller than
the others. If it corresponds to one of the additional
parameters, then this parameter should be transposed into an
independent variables, so as to improve the conditionality of the
matrix Jw ,which leads to the non-uniqueness of the solution. If
this is impossible, then such singular numbers should be assumed
to be zero, giving a tendency to stability of the system solution
. Practically these operation are equivalent to keeping constant
weak parameters which cannot be reliably determined from the
given experiment. In program we have assumed zero such i for
which i/ max < R, where R reflects the relative accuracy of
the initial data. Thus the application of the singular
decomposition represents valuable information on the reliability
and sensitivity of the determined parameters.
The principal suggestion, allowing use of the least-squares
method, is that the errors in the measurement are random
variables and subordinate the normal distribution law. In this
case the errors of measurement F are formed from the smaller
errors i, their dispersion being almost the same, while the
distribution law for each of them is unrestricted. Thus, correct
application of the least-squares method must use the weight
factor which is calculated using the dispersions of both the
observed value and the independent variable according to the law
of error distribution. Hence, in our program we use the weight
factors calculated as follows:
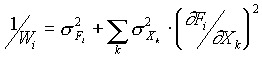
where the summation extends to all the independent variables.
It should be noted that the weight factors calculated according
to this formula will depend on the refined parameters, so they
should be calculated for every iteration.
The user has a choice of 3 weighting schemes.
Thus, we obtain a statistically rigorous scheme of refinement
of equilibrium constants and the additional parameters using the
non-linear least-squares method.
In conclusion, the program SIRKO presents the following set of advantages with respect to the already existing programs:
The polyvalence of SIRKO, usable for any of the three types of experiments, and its interactivity, make of SIRKO the best of all the programs we have used for our calixarene studies.